載入中...

AI 概論與實作入門

發表於2024-01-01|更新於2025-11-28|筆記AI

|總字數:39|閱讀時間:1分鐘|瀏覽量:|評論數:

本篇文章連結：https://4yu.dev/post/AI

目前僅有簡報版本，尚未整理成筆記文章

https://slides.com/shiyu/ai 🔗

AI 簡報總覽

AI 目錄 1
AI 目錄 2

回到導覽頁面

文章作者: ShiYu Huang

文章連結: https://4yu.dev/post/AI/

版權聲明: 本部落格所有文章除特別聲明外，均採用CC BY-NC-SA 4.0 授權協議。轉載請註明來源 4yu Blog！

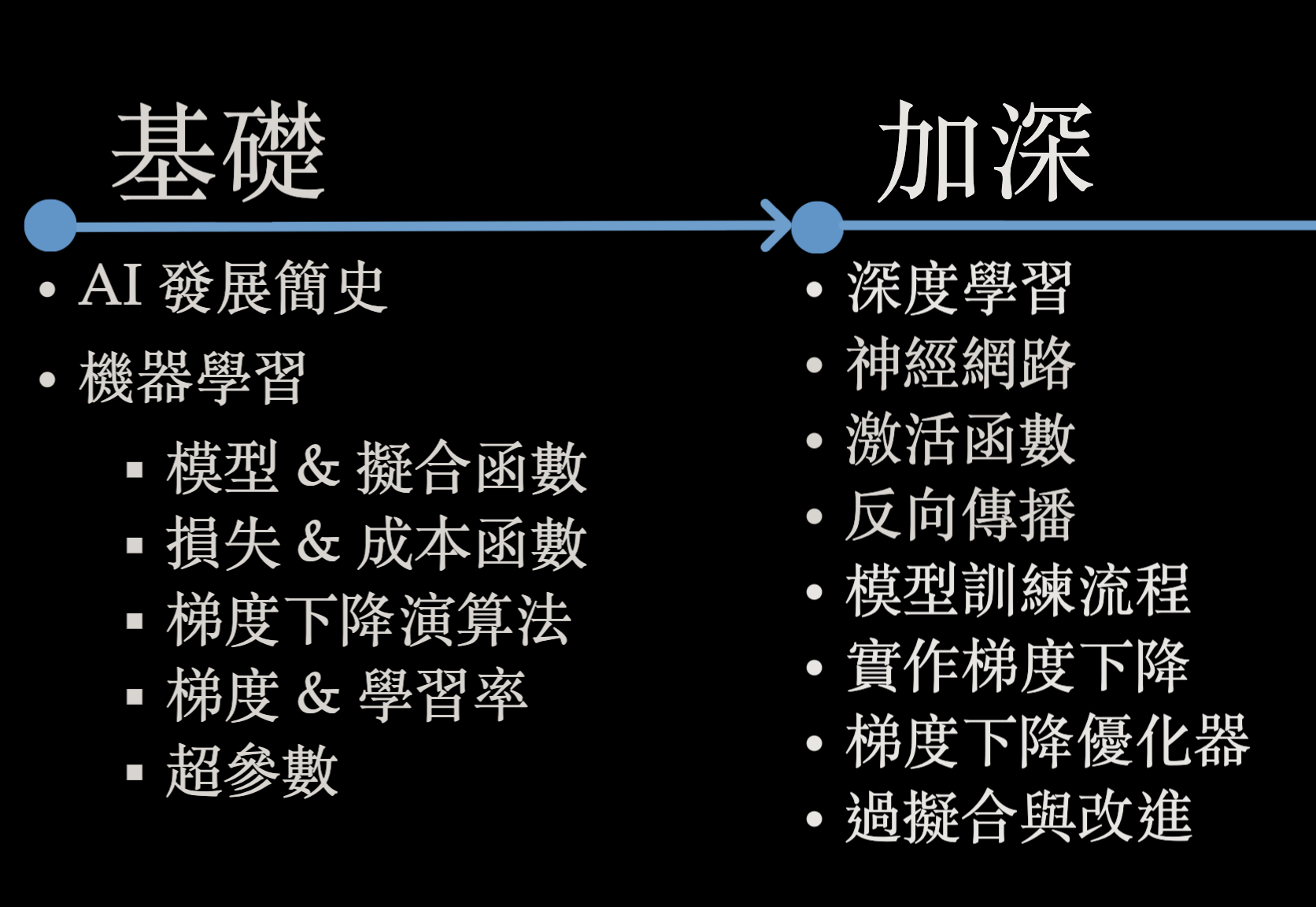
機器學習 ML 深度學習 DL 卷積神經網路 CNN Transformer GPT 強化學習 Reinforcement Learning 神經網路 Neural Network 損失函數 Loss Function 梯度下降演算法 Gradient Descent 擬合函數 Fitting Function 過擬合 Overfiting 感知器 Perceptron 多層感知器 MLP 全局最小值 Global Minima 學習率 Learning Rate 偏微分 Partial Derivative 超參數 Hyperparameter 激活函數 Activity Function 反向傳播演算法 Backward Propagation 鏈式法則 Chain Rule 監督式學習 Supervised Learning 均方誤差 MSE 均方根誤差 RMSE 平均絕對值誤差 MAE 交叉熵 Cross-Entropy 模擬退火演算法 Simulated Annealing 遺傳演算法 Genetic Algorithm 粒子群演算法 PSO 隨機梯度下降 SGD 優化器 Optimizer Newton’s Method Momentum Nesterov (NAG)AdaGrad RMSprop Adam Nadam Dropout 線性迴歸邏輯迴歸決策樹決策森林 KNN SVM DQN Policy-based Actor-Critic TD-Learning PPO A2C Baseline Softmax U-Net 殘差網路 ResNet RNN LSTM GRU BERT 詞嵌入 Embedding 注意力機制 Attention Fine-Tuning LoRA RLHF Hallucination 檢索增強生成 RAG Prompt Engineering CoT ViT Positional Encoding 生成對抗網路 GAN AutoEncoder VAE Diffusion 擴散模型評分函數 Score Function Stable Diffusion Sora AlphaGO AlphaFold FSD AGI 對抗樣本攻擊 Adversarial Attack 提示詞注入攻擊 Prompt Injection Attack Jailbreaking NVQLink 量子退火 Quantum Annealing AI Agent MCP Vibe Coding

相關推薦

訓練神經網路計算過程

這是一個具有一層隱藏層的神經網路：假設 🔗 輸入層有 3 個節點，輸入 X 中有 3 筆數據，其標籤為 Y： X=[1202−32−1−13],Y=[12−3] X = \begin{bmatrix} 1 & 2 & 0 \\ 2 & -3 & 2 \\ -1 & -1 & 3 \\ \end{bmatrix}, Y = \begin{bmatrix} 1 \\ 2 \\ -3 \\ \end{bmatrix} W1=[−10−111−1] W_1 = \begin{bmatrix} -1 & 0 \\ -1 & 1 \\ 1 & -1 \\ \end{bmatrix} 隱藏層有 2 個節點，隱藏層權重矩陣為 W1W_1，線性組合 Z=XW1Z=XW_1，經過激活函數 σ\sigma 後的值為 KK，即 K=σ(Z)K = \sigma(Z) 另激活函數 σ\sigma 為 ReluRelu 函數， σ(x)=Relu(x)=max(x,0)\sigma(x)=Relu(x)=max(x,0) 輸出層有 1 個節點，其權重矩陣為 W2W_2，線性輸出 O=KW2O=KW_2 W2=[1−2] W_2 = \begin{bmatrix} 1 \\ -2 \\ \end{bmatrix} 將輸出值與標籤去計算損失，令損失為 JJ，假設使用加總型式的最小平方損失 J=∑(12(O−Y)2)J = \sum (\frac{1}{2}(O-Y)^2) 此時，已知輸出層梯度： Gout=∂J∂O=O−YG_{out} = \frac{\partial J}{\partial O}=O-Y 隱藏層梯度： G2=∂J∂W2=∂J∂O∂O∂W...

評論